📈 Big O

On a mathematical tool used to calculate time complexity in software algorithms.

Also known as Landau's notation, it allows for measuring the speed of a given function based on the specifics of its implementation, where O is the rate of growth of the function, standing for its order of approximation. This effectively allows for easier comparison of the implementations, ultimately making it possible to deliver an optimal solution for a given problem.

Complexity

Big O notation measures the complexity of an algorithm by measuring the input to output execution rate. This rate takes into account programming concepts and elements such as loops and conditional statements.

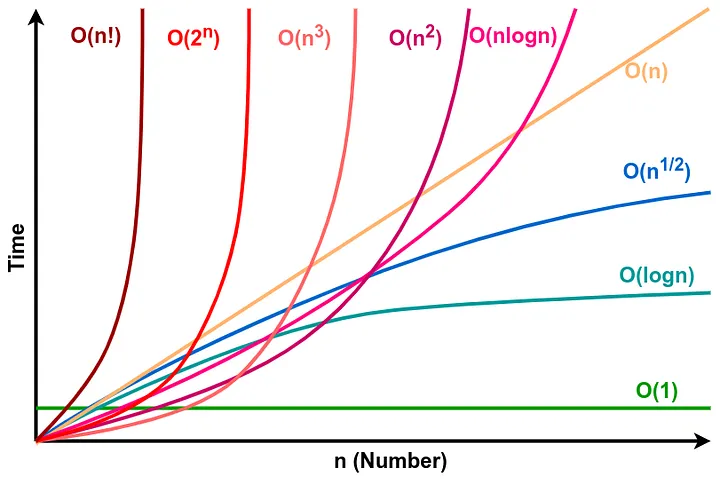
In general, the fewer elements you have, the faster the execution rate and, thus, the simpler the notation. For Big O, many time complexities exist; however, these six are considered to be the main ones and are encountered most commonly:

• O(1) Constant Time
• O(n) Linear Time
• O(log n) Logarithmic Time
• O(n²) Quadratic Time
• O(2ⁿ) Exponential Time
• O(n!) Factorial Time

As can be seen from the chart, time complexities differ in performance, and thus, the goal is to optimize the implementation to be as simple as possible.

JavaScript is used for the appropriate examples.

O(1) Constant Time

Constant time algorithms are independent of the input and therefore always execute with the exact same speed.

Check if a number is even or odd.

const isEven = n => n % 2 === 0;

That's because this function has only a single execution step.

O(n) Linear Time

Linear time algorithms are linearly dependent on the input. As in, as the input increases in size, so does the number of execution steps required.

Sum all the values in an array.

const sumArray = n => n.reduce((sum, value) => sum + value, 0);

O(log n) Logarithmic Time

Logarithmic time algorithms are dependent on the logarithm of the input, meaning that the execution steps decrease as the input size increases.

Searching through a binary search tree.

const searchBST = (node, n) => {
  if (!node || node.value === n) return node;
  return n < node.value ? searchBST(node.left, n) : searchBST(node.right, n);
};

O(n²) Quadratic Time

Quadratic time algorithms double in their execution steps. This commonly happens due to operations such as nested loops.

Checking for duplicate elements in an array.

const hasDuplicates = n => {
  for (const i in n)
    for (const j in n)
      if (i !== j && n[i] === n[j]) return true;
  return false;
};

O(2ⁿ) Exponential Time

Exponential time algorithms increase in execution steps exponentially depending on the size of the input. This often happens with recursive functions, a classic example of which is shown below.

Find the nth Fibonacci number.

const fibonacci = n => {
  if (n <= 1) return n;
  return fibonacci(n - 1) + fibonacci(n - 2);
};

O(n!) Factorial Time

Factorial time algorithms have execution steps that grow factorially with the size of the input. This results in the worst performance possible.

Generate all permutations of an array.

const permuteArray = n => {
  const result = [];

  const permutate = (currArr, remainArr) => {
    if (remainArr.length === 0) result.push(currArr);
    else
      for (let i = 0; i < remainArr.length; i++)
        permutate(
          [...currArr, remainArr[i]],
          [...remainArr.slice(0, i), ...remainArr.slice(i + 1)]
        );
  };

  permutate([], n);
  return result;
};

This concludes a brief explanation of the mathematical concept of Big O notation and its implications in software development.

Happy Coding!